해시 함수를 사용해서 변환한 값을 인덱스로 삼아 키와 값을 저장
⇒ 빠른 데이터 탐색을 제공하는 자료구조다.
사실, JS에서 **객체(Object)**나 Map을 사용해서 키-값 쌍을 저장하는 방식을 해시테이블이라 부른다.
해시 구조는 이렇게 4가지임
- 키(Key): 저장하고 싶은 데이터의 식별자
- 해시함수(Hash Function): 키를 입력받아 해시 인덱스를 계산해주는 함수
- 해시 인덱스(Hash Index): 해시함수가 계산해낸 고정된 범위의 인덱스
- 값(Value): 실제 저장하고 싶은 데이터
해시함수란? ⇒ 임의의 크기의 데이터를 입력받아 고정된 크기의 해시 값으로 변환해주는 함수
해시함수는 마치 현장에서 자재 하나하나에 고유 번호를 붙여서 관리하는 것과 비슷하다.
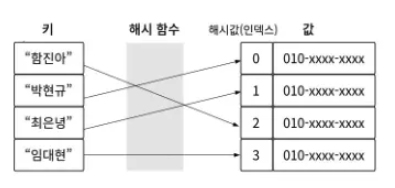
키 → 해시 함수를 통해 계산 → 해시 인덱스 → 이 인덱스에 대응하는 값
해시 특징부터
특징
- 해시는 단방향으로 동작한다.(키를 통해 값 찾기 o , 값을 통해 키 찾기 x) ← O(1)
- 입력 값이 조금만 달라도 완전히 다른 해시 값을 생성함
- 해시 값의 길이는 고정되어 있어, 대량의 데이터를 효율적으로 관리 가능
- 서로 다른 입력이 같은 해시 값을 가질 수도 있는데, 이를 충돌이라고 하며, 충돌을 최소화하는 게 중요한 포인트다.
해시 테이블 : 키와 대응한 값이 저장되어 있는 공간
버킷 : 해시 테이블의 각 데이터
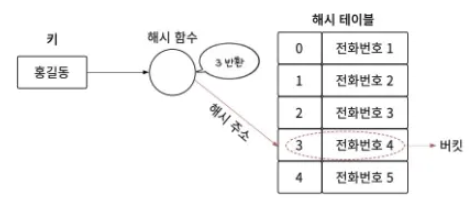
해시는 언제 쓰냐면
- 비밀번호 관리
- 데이터베이스 인덱싱
- 블록체인
일단 자바스크립트에선 해시를 노출하지 않습니다.
대신 오브젝트(객체)라는 자료형을 제공하는데 이 자료형은 해시와 거의 동일하게 동작하므로 해시를 쉽게 사용할 수 있음
⇒ 값이 변하면 안돼요.
해시 함수를 구현할 때 고려할 내용
1. 해시 함수가 변환한 값은 인덱스로 활용해야 하므로 해시테이블의 크기를 넘으면 안된다.
2.해시 함수가 변환한 값의 충돌은 최대한 적게 발생해야 한다.
자주 쓰는 해쉬함수를 알아보겠다.
해시 기법 공식 장점 단점
| 나눗셈법 (Division Method) | h(k) = k % m | 간단, 빠름 | m 값이 나쁘면 충돌 많음 |
| 곱셈법 (Multiplication Method) | h(k) = ⌊m * (k * A % 1)⌋ | 소수를 안 써도 충돌 적음 | A 값 잘 골라야 함 |
| 문자열 해싱 (String Hashing) | h(s) = Σ(ord(s[i]) * p^i) % m | 충돌 적고 문자열 비교 가능 | p, m 선택이 중요 |
k : 키 값
m : 해시 테이블 크기(소수로 설정하면 충돌이 줄어 듦)
A: 0과 1 사이의 적절한 실수 (일반적으로 A≈0.6180339887 사용)
A≈0.6180339887A \approx 0.6180339887
s_i: 문자열의 i번째 문자
p: 적절한 소수 값 (보통 31이나 37 사용)
1. 나머지 법(Division Method)
📌 개념:
- 해시 값을 구할 때 특정한 소수(prime number)로 나누고 나머지를 사용하는 방식
- 주로 소수(Prime Number)를 사용하면 충돌이 적게 발생해서 효율적이다.
🔹 해시 함수 공식: h(k) = k % m
- k: 키 값
- m: 해시 테이블 크기 (소수로 설정하면 충돌이 줄어듦!)
소수 : 1과 자기 자신만을 약수로 가지는 자연수
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, ... (무한히 많음)
// [10,20,30]
// [100]
// h(k) = 10 % 100 = 0 => 0번째 해시테이블에 저장
// h(k) = 11 % 100 = 1 => 1번째 해시테이블에 저장
// h(k) = 20 % 100 = 0 => 0번째 해시테이블에 저장 => 충돌! => 방법 2개중에 택해서 사용
🔹 예제 코드 (Python)
def division_hash(key: int, size: int) -> int:
return key % size # 나머지를 인덱스로 사용
size = 7 # 해시 테이블 크기 (소수로 선택)
print(division_hash(50, size)) # 50 % 7 = 1
print(division_hash(23, size)) # 23 % 7 = 2
print(division_hash(99, size)) # 99 % 7 = 1 (충돌 발생)
장점: 구현이 간단하고 계산 속도가 빠름.
단점
- 키 값이 특정한 패턴을 가지면 충돌이 많이 발생할 수 있음.
- 그래서 소수를 선택해야 충돌을 줄일 수 있다.
2. 곱셈법(Multiplication Method)
📌 개념:
- 특정한 상수 값을 곱하고 소수 부분만 사용하는 방식
- 이 방법은 소수를 사용할 필요가 없고, 충돌이 적음.
- 컴퓨터의 비트 연산(shift)을 활용할 수 있어서 빠름!
🔹 해시 함수 공식: h(k) = ⌊m * (k * A % 1)⌋
- k: 키 값
- m: 해시 테이블 크기 (소수로 설정하면 충돌이 줄어듦!)
- A: 0과 1 사이의 적절한 실수 (일반적으로 A≈0.6180339887 사용)
🔹 예제 코드 (Python)
def multiplication_hash(key: int, size: int) -> int:
A = 0.6180339887 # 일반적으로 많이 쓰이는 값 (황금 비율)
return int(size * ((key * A) % 1)) # 소수 부분만 사용
size = 10 # 해시 테이블 크기
print(multiplication_hash(50, size)) # 결과 예측 어려움
print(multiplication_hash(23, size))
print(multiplication_hash(99, size))
장점:
- 소수를 안 써도 충돌이 적음.
- 연산이 빠름! (비트 연산 활용 가능)
단점:
- A 값을 적절히 선택해야 함.
3. 문자열 해싱(String Hashing)
📌 개념:
- 문자열을 숫자로 변환하는 방식이다.
- 각 문자의 아스키(ASCII) 값을 사용해서 해시 값을 만든다.
- 여러 개의 문자를 하나의 숫자로 변환해야 하므로 보통 다항식(poly) 해싱을 사용한다.
🔹 해시 함수 공식 (Polynomial Hashing) : h(s) = Σ(ord(s[i]) * p^i) % m
- h(s) : 문자열 s의 해시 값. (결과값)
- Σ (시그마,summation)
- 이건 **합(sum)**을 나타내는 수학 기호
- • 여기선 문자열의 각 문자를 숫자로 변환한 값을 더하는 역할
- ord(s[i]) : 문자의 숫자 변환
- s_i: 문자열의 i번째 문자
- p: 적절한 소수 값 (보통 31이나 37 사용)
- p^i : 거듭제곱. p를 i번 곱함
- m: 해시 테이블 크기
- 각 문자를 숫자로 바꾸고,
- 그 숫자에 p^i(거듭제곱) 곱해서 다 더한 다음,
- 해시 테이블 크기로 나눠서 해시 값 만든다
🔹 예제 코드 (Python)
def polynomial_string_hash(s: str, size: int) -> int:
p = 31 # 보통 31, 37, 53 같은 소수를 선택
hash_value = 0
for i, char in enumerate(s):
hash_value += (ord(char) * (p ** i)) # 다항식 해싱
return hash_value % size # 테이블 크기에 맞게 나머지 연산
size = 1000 # 해시 테이블 크기
print(polynomial_string_hash("hello", size)) # 해시 값
print(polynomial_string_hash("Hello", size)) # 다른 값이 나옴
⚡ 장점:
- 문자열의 순서를 고려할 수 있어서 충돌이 적음.
- 보통 p를 소수로 설정하면 충돌이 더 줄어듦.
⚡ 단점:
- p와 m 값을 적절히 선택하지 않으면 충돌이 많아질 수 있음.
- 문자열 길이가 길면 계산량이 많아질 수 있음.
1️⃣ 숫자 키(hash key):
- 해시 테이블 크기가 소수라면 → 나눗셈법
- 소수 설정 없이 하고 싶다면 → 곱셈법
2️⃣ 문자열 해싱
- 짧은 문자열이면 다항식 해싱(poly hash)
- 긴 문자열이면 SHA-256 같은 보안 해싱을 고려
💡 결국, 해시 함수는 "충돌을 얼마나 줄일 수 있는가?"가 가장 중요하다.
그래서 m, A, p 값을 어떻게 선택하느냐에 따라 성능 차이가 생길 수 있다.
충돌은 왜 발생하는 걸까!?
해쉬 함수에서 mod연산( / 나머지 연산)을 사용하면 일정한 패턴으로 값이 반복 된다.
즉, 어떤 수 m으로 mod연산을 하면 그 범위 안에서만 해쉬 값이 나올 수 밖에 없음.
• 50 % 7 = 1
• 99 % 7 = 1
• 148 % 7 = 1
• 197 % 7 = 1
즉 , 7씩 증가하는 값들은 계속 같은 값을 갖게 되는 것이다.
이걸 수식어로 정리하면
k = x(인덱스값) % m (해시테이블)
x라는 숫자는 m을 주기로 반복됨
✅ 1. 해시 함수에서 mod 연산 후 동작 원리
해시 함수에서 mod 연산을 하면, 값이 특정한 범위 안에만 존재하게 된다.
즉,
x \mod 3
이렇게 하면 가능한 해시 값은 항상 0, 1, 2 중 하나다.
해시 테이블 크기가 3이라면 해시 값이 3이 나올 수가 없다!
📌 예제
console.log(6 % 3); // 0
console.log(9 % 3); // 0
console.log(12 % 3); // 0
console.log(7 % 3); // 1
console.log(10 % 3); // 1
console.log(11 % 3); // 2
✅ 2. 해시 테이블에서 저장 방식
만약 해시 테이블 크기가 3이라면,
저장되는 위치는 항상 0, 1, 2번 칸 중 하나야.
📌 충돌이 발생하면?
• 6, 9, 12 → 전부 0번 인덱스
• 7, 10, 13 → 전부 1번 인덱스
• 8, 11, 14 → 전부 2번 인덱스
이렇게 되면 같은 인덱스에 저장될 가능성이 커서 충돌이 많아진다.
그래서 해시 테이블 크기를 소수(Prime Number)로 설정하는 게 충돌을 줄이는 핵심 전략이다.
✅ 3. 만약 해시 값이 3이 나오면 바로 멈춰?
💡 여기서 중요한 점:
✔ 해시 값은 해시 테이블 크기보다 작아야 해!
✔ mod 연산을 하면 해시 값이 테이블 크기(m)보다 클 수가 없음.
✔ 즉, 해시 값이 3이 나오면 “멈출 필요 없이” 처음부터 0~m-1 범위에서 나옴!
즉, x % 3을 하면 결과는 0, 1, 2 중 하나이므로, 3이 나오지 않음
✔ “멈추냐”를 고민할 필요가 없는 거지
✅ 4. 만약 해시 테이블 크기가 3이 아니라 10이라면?
console.log(6 % 10); // 6
console.log(9 % 10); // 9
console.log(12 % 10); // 2
console.log(7 % 10); // 7
console.log(10 % 10); // 0
console.log(11 % 10); // 1
✔ 이 경우에는 0~9 범위에서 해시 값이 결정됨!
✔ 3이 나올 수도 있고, 6도 나올 수도 있고, 9도 나올 수 있음!
📌 즉, x % m에서 m이 몇이냐에 따라 해시 값 범위가 결정됨!
✔ x % 3의 결과는 항상 0, 1, 2 중 하나!
✔ 해시 테이블 크기가 3이면 해시 값이 3이 나올 수가 없음.
✔ 즉, “멈추냐”를 고민할 필요 없이 처음부터 0~m-1 범위에서 값이 나옴!
✔ 그래서 해시 충돌을 줄이려면 테이블 크기를 소수(Prime Number)로 설정하는 게 중요함!
충돌 처리
해시 테이블에서 충돌은 다른 키가 같은 해시 값(인덱스)을 가질 때 발생하는 문제다.
해시 함수가 아무리 좋아도 충돌은 피할 수 없으므로, 충돌 해결 방법이 필요하다.
✅ 충돌 해결 방법은 크게 2가지
🔹 1. 체이닝(Chaining, Separate Chaining)
🔹 2. 개방 주소법(Open Addressing)
✅ 1. 체이닝(Chaining) 방식
📌 개념
- 배열이나 연결리스트 같은 것을 활용해 이중 데이터구조를 쓰는 것
- 같은 해시 값을 가지는 데이터를 연결 리스트(Linked List)로 저장하는 방식
- 충돌이 발생하면 해당 인덱스에 새로운 데이터를 추가(append)하면 됨!
📌 예시 (해시 테이블 크기: 5)
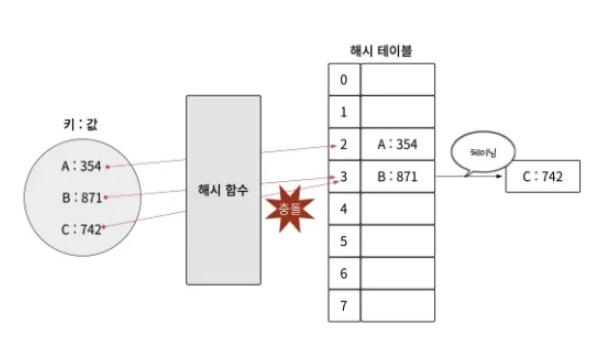
해시 함수: h(k) = k % 5
데이터: [10, 20, 25, 30]
0: [10, 20] ← 같은 해시 값이라 리스트로 저장
1: [ ]
2: [25]
3: [30]
4: [ ]
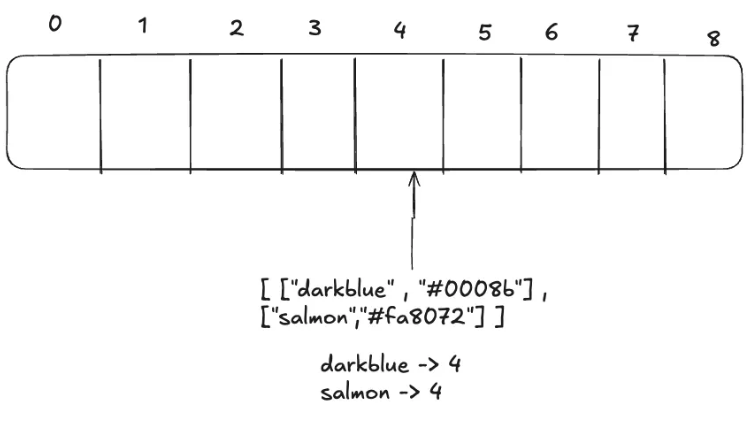
4에 같이 저장되는 거임. 첫번째 요소, 두번째 요소
충돌이 발생하면 해시 값이 같은 데이터를 같은 인덱스에 리스트로 저장하면 해결됨
📌 JavaScript 코드 (체이닝)
class HashTable {
constructor(size) {
this.size = size;
this.table = new Array(size).fill(null).map(() => []); // 각 인덱스에 배열(리스트) 저장
}
hashFunction(key) {
return key % this.size;
}
insert(key, value) {
const index = this.hashFunction(key);
this.table[index].push([key, value]); // 같은 인덱스에 여러 개 저장 가능
}
search(key) {
const index = this.hashFunction(key);
for (let [k, v] of this.table[index]) {
if (k === key) return v;
}
return null;
}
}
// 테스트
const ht = new HashTable(5);
ht.insert(10, "A");
ht.insert(20, "B"); // 충돌 발생 → 같은 리스트에 추가
ht.insert(25, "C");
ht.insert(30, "D");
console.log(ht.search(10)); // "A"
console.log(ht.search(20)); // "B"
console.log(ht.search(25)); // "C"
console.log(ht.search(99)); // null (없는 값)
📌 체이닝의 장점과 단점
체이닝 방식 설명
| 장점 | 1. 충돌이 많아도 리스트에 추가 가능 |
| 2. 해시 테이블 크기가 꽉 차도 새로운 데이터 삽입 가능 | |
| 단점 | 1. 같은 해시 값이 많아지면 검색 속도가 느려짐 (O(n)) |
| 2. 연결 리스트를 저장해야 해서 메모리 사용량이 많을 수 있음 |
✅ 2. 개방 주소법(Open Addressing)
📌 개념
- 충돌이 발생하면 해시 테이블 내에서 빈 공간을 찾아 저장하는 방식
- 즉, 테이블 안에서 충돌을 해결하려고 하는 방식!
- 추가적인 리스트(메모리)가 필요 없음!
📌 3가지 주요 기법
- 선형 탐사 (Linear Probing) → 충돌 발생 시 다음 빈 칸을 순차적으로 찾아 저장하는 방법.
- 이차 탐사 (Quadratic Probing) → 충돌 발생 시 제곱수(1², 2², 3²…)만큼 이동하여 빈 칸을 찾는 방법.
- 이중 해싱 (Double Hashing) → 충돌 발생 시 다른 해시 함수를 한 번 더 사용하여 빈 칸을 찾는 방법.
✅ (1) 선형 탐사 (Linear Probing)
📌 개념
- 충돌 발생 시, 다음 빈 공간을 순차적으로 찾아서 저장하는 방식
- 해시 값이 이미 차 있으면 (충돌횟수 +1), (인덱스 +2) 이렇게 계속 이동
📌 예시 (해시 테이블 크기: 5)
해시 함수: h(k) = k % 5
데이터: [10, 20, 25, 30]
0: 10
1: 20
2: 25 ❌ (충돌 발생) → 다음 빈칸(3)으로 이동
3: 25
4: 30
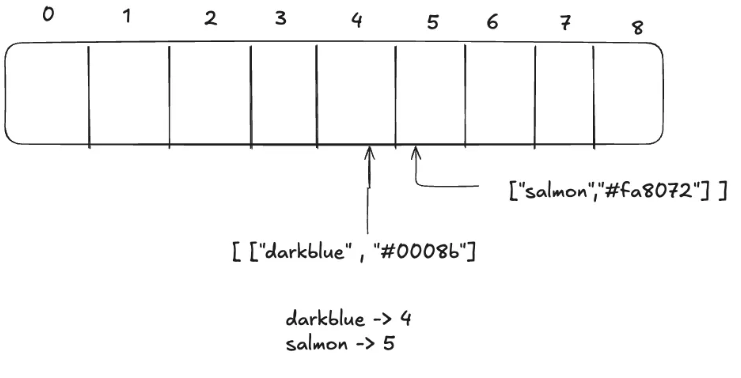
✔ 충돌이 발생하면 "다음 빈 자리"를 찾아가면서 저장한다!
📌 JavaScript 코드 (선형 탐사)
class HashTable {
constructor(size) {
this.size = size;
this.table = new Array(size).fill(null);
}
hashFunction(key) {
return key % this.size;
}
insert(key, value) {
let index = this.hashFunction(key);
while (this.table[index] !== null) { // 충돌 발생 시 다음 칸으로 이동
index = (index + 1) % this.size;
}
this.table[index] = [key, value]; // 빈 공간 찾으면 저장
}
search(key) {
let index = this.hashFunction(key);
while (this.table[index] !== null) {
if (this.table[index][0] === key) {
return this.table[index][1];
}
index = (index + 1) % this.size;
}
return null; // 찾는 값이 없으면 null 반환
}
}
✔ 선형 탐사는 충돌 해결이 간단하지만, 클러스터링(데이터 몰림) 문제가 발생할 수 있음!
✅ (2) 이차 탐사 (Quadratic Probing)
- 충돌 발생 시, 1², 2², 3²... 이렇게 제곱수만큼 이동하는 방식
- h(k) = (해시 값 + i²) % 테이블 크기
📌 예시
해시 함수: h(k) = k % 5
데이터: [10, 20, 25, 30]
0: 10
1: 20
2: 25 ❌ (충돌 발생) → 1²(1)만큼 이동 → 3번 칸 저장
3: 25
4: 30 ❌ (충돌 발생) → 1²(1) 이동(3번), 이미 차 있음 → 2²(4) 이동 → 4번 칸 저장
예시
새 인덱스 = (기본 해시 값+i^2 ) % 테이블 크기
- 기본해시값 = k
- i = 충돌회수
[2차 탐사 기본 원리]
해시 테이블에 데이터를 넣을 때, 만약 계산된 초기 인덱스에 이미 다른 값이 있다면 충돌이 발생합니다.
이때 선형 탐사는 바로 다음 인덱스(즉, +1씩)로 이동하지만,
2차 탐사는 이동 거리를 제곱수(i²)로 증가시키면서 빈 슬롯을 찾습니다.
예를 들어 ,
해시 함수가 h(k) = k % 5라고 가정하고,
데이터가 [10, 20, 25, 30]이라고 해보겠습니다.
보통 이렇게 진행됩니다:
- 10 삽입:
- h(10) = 10 % 5 = 0
- 슬롯 0이 비었으니, 10을 슬롯 0에 저장합니다.
- 20 삽입:
- h(20) = 20 % 5 = 0 → 슬롯 0은 이미 10으로 채워져 있으니 충돌!
- 첫 번째 탐사: i = 1, 이동 거리 = 1² = 1→ 새로운 인덱스: (0 + 1) % 5 = 1
- 슬롯 1이 비었으니, 20을 슬롯 1에 저장합니다.
- 25 삽입:
- h(25) = 25 % 5 = 0 → 슬롯 0 충돌!
- i = 1: (0 + 1²) % 5 = 1 → 슬롯 1도 이미 20으로 채워져 있으니 충돌!
- i = 2: (0 + 2²) % 5 = (0 + 4) % 5 = 4
- 슬롯 4가 비었으니, 25를 슬롯 4에 저장합니다.
- 30 삽입:
- h(30) = 30 % 5 = 0 → 슬롯 0 충돌!
- i = 1: (0 + 1²) % 5 = 1 → 슬롯 1 충돌!
- i = 2: (0 + 2²) % 5 = 4 → 슬롯 4 충돌!
- i = 3: (0 + 3²) % 5 = (0 + 9) % 5 = 4 → 여전히 슬롯 4, 충돌!
- i = 4: (0 + 4²) % 5 = (0 + 16) % 5 = 1 → 슬롯 1, 충돌!
- … 이런 식으로 진행되면서, 만약 빈 슬롯(예: 슬롯 2나 3)이 있다면 거기로 저장할 수 있습니다.(실제 구현에서는 테이블의 크기와 탐사 규칙에 따라 빈 슬롯을 찾도록 설계합니다.)
[코드 예제]
function quadraticProbeInsert(hashTable, key, tableSize) {
let initialIndex = key % tableSize; // 처음 인덱스
let i = 0; // 충돌 회수
let index; // 인덱스 변수만 설정
while (i < tableSize) {
// 2차 탐사: 이동 거리는 i²
index = (initialIndex + i * i) % tableSize;
if (hashTable[index] === undefined) {
hashTable[index] = key;
return index;
}
i++;
}
throw new Error("해시 테이블이 가득 찼습니다!");
}
const tableSize = 5;
let hashTable = new Array(tableSize);
console.log("10 삽입 위치:", quadraticProbeInsert(hashTable, 10, tableSize)); // 10 % 5 = 0 → 슬롯 0
console.log("20 삽입 위치:", quadraticProbeInsert(hashTable, 20, tableSize)); // 충돌 후 슬롯 1
console.log("25 삽입 위치:", quadraticProbeInsert(hashTable, 25, tableSize)); // 충돌 후 슬롯 4
// 30 삽입 예제 (빈 슬롯이 있다면 그곳에 저장됨)
try {
console.log("30 삽입 위치:", quadraticProbeInsert(hashTable, 30, tableSize));
} catch(e) {
console.log("30 삽입 실패:", e.message);
}
console.log("최종 해시 테이블:", hashTable);
[요약]
- 초기 인덱스 = h(k)
- 만약 충돌이면, 차례대로 h(k) + 1², h(k) + 2², h(k) + 3², …를 계산하여 빈 슬롯을 찾는 방식입니다.이렇게 하면 선형 탐사보다 연속된 슬롯에 데이터가 몰리는 클러스터링 현상이 줄어들 수 있습니다.
✔ 선형 탐사보다 클러스터링이 적음!
✅ (3) 이중 해싱 (Double Hashing)
충돌이 발생했을 때, 다른 해시 함수를 한 번 더 적용해서 이동할 거리(증가값)를 계산하는 방식
- 기본 해시 함수: h1(k) = k % 테이블 크기
- 보조 해시 함수: h2(k) = 1 + (k % 보조 소수)
- 이동 규칙: 새 인덱스 = (h1(k) + i * h2(k)) % 테이블 크기
이중 해싱 예제
📌 해시 테이블 크기: 7
✅ 데이터 삽입: [10, 20, 30, 40]
- 10 삽입
- h1(10) = 10 % 7 = 3 → 슬롯 3에 삽입 (충돌 없음)
- 20 삽입
- h1(20) = 20 % 7 = 6 → 슬롯 6에 삽입 (충돌 없음)
- 30 삽입
- h1(30) = 30 % 7 = 2 → 슬롯 2에 삽입 (충돌 없음)
- 40 삽입
- h1(40) = 40 % 7 = 5 → 슬롯 5에 삽입 (충돌 없음)
- 50 삽입 (충돌 발생!)
- h1(50) = 50 % 7 = 1 → 슬롯 1에 삽입하려는데 충돌 발생!
- h2(50) = 1 + (50 % 5) = 1 + 0 = 1
- 새로운 위치: (1 + 1 * 1) % 7 = 2 → 슬롯 2도 차있음!
- 다음 이동: (1 + 2 * 1) % 7 = 3 → 슬롯 3도 차있음!
- 다음 이동: (1 + 3 * 1) % 7 = 4 → 슬롯 4가 비어있음 → 저장!
📌 예시
해시 함수: h(k) = k % 5
보조 해시 함수: h2(k) = 1 + (k % 4)
데이터: 10, 20, 25, 30
0: 10
1: 20
2: 25 ❌ 충돌 발생 → h2(25) = 2칸 이동 → 4번 칸 저장
3:
4: 25
✔ 충돌이 적고 탐색 속도가 빠름!
🎯 정리
방법 충돌 해결 방식 특징
| 체이닝 | 연결 리스트로 같은 인덱스 관리 | 메모리 추가 사용 |
| 선형 탐사 | 다음 빈 공간 순차 탐색 | 클러스터링 문제 |
| 이차 탐사 | 제곱수만큼 이동 | 성능 개선 |
| 이중 해싱 | 다른 해시 함수로 이동 | 충돌 최소화 |
Set,Map으로 해시테이블 만들어보기
1️⃣ Set (집합)
- 중복을 허용하지 않는 데이터 구조
- 값만 저장 (키-값 쌍이 아님)
- 빠른 탐색 가능 (해시 기반)
// 📌 해시 테이블 클래스 정의
class HashTable {
constructor() {
// JavaScript의 Map 객체를 사용하여 내부적으로 해시 테이블을 구현
// Map은 키-값 저장이 가능하고, 중복된 키를 허용하지 않음
this.map = new Map();
}
// 📌 데이터를 삽입하는 함수
insert(key, value) {
this.map.set(key, value); // 키-값을 저장 (이미 존재하는 키면 값을 덮어씀)
}
// 📌 특정 키의 값을 가져오는 함수
get(key) {
return this.map.get(key); // 해당 key가 존재하면 값을 반환, 없으면 undefined 반환
}
// 📌 특정 키를 삭제하는 함수
delete(key) {
this.map.delete(key); // 해당 key가 존재하면 삭제
}
// 📌 현재 해시 테이블의 모든 데이터를 출력하는 함수
print() {
console.log(this.map); // Map 객체 전체를 출력
}
}
// ✅ 해시 테이블 객체 생성
const table = new HashTable();
// ✅ 데이터 삽입 (키-값 저장)
table.insert("apple", "사과"); // "apple" → "사과" 저장
table.insert("banana", "바나나"); // "banana" → "바나나" 저장
table.insert("grape", "포도"); // "grape" → "포도" 저장
// ✅ 특정 키의 값 가져오기
console.log(table.get("apple")); // 출력: "사과"
// ✅ 특정 키 삭제
table.delete("banana");
// ✅ 현재 저장된 전체 데이터 출력
table.print(); // 출력: Map { 'apple' => '사과', 'grape' => '포도' }
Map을 이용한 해시 테이블
class HashTable {
constructor() {
// 📌 Map을 이용해서 내부적으로 해시 테이블을 구현
// Map은 키-값 저장이 가능하며, 중복된 키를 허용하지 않음
this.map = new Map();
}
// 📌 데이터를 추가하는 함수
insert(key, value) {
this.map.set(key, value); // key-value 쌍을 저장
}
// 📌 특정 키에 대한 값을 가져오는 함수
get(key) {
return this.map.get(key); // 해당 key가 있으면 값을 반환, 없으면 undefined 반환
}
// 📌 특정 키를 삭제하는 함수
delete(key) {
this.map.delete(key); // 해당 key 삭제
}
// 📌 현재 해시 테이블의 모든 데이터를 출력하는 함수
print() {
console.log(this.map); // Map 객체를 콘솔에 출력
}
}
// ✅ 해시 테이블 객체 생성
const table = new HashTable();
// ✅ 데이터 삽입 (키-값 저장)
table.insert("apple", "사과"); // "apple" → "사과"
table.insert("banana", "바나나"); // "banana" → "바나나"
table.insert("grape", "포도"); // "grape" → "포도"
// ✅ 특정 키의 값 가져오기
console.log(table.get("apple")); // "사과"
// ✅ 특정 키 삭제
table.delete("banana");
// ✅ 현재 저장된 전체 데이터 출력
table.print(); // Map { 'apple' => '사과', 'grape' => '포도' }
📌 코드 설명
- constructor() (생성자)
- this.map = new Map(); → 자바스크립트의 Map 객체를 사용하여 해시 테이블을 만듦.
- Map은 키-값 형태로 데이터를 저장할 수 있음.
- insert(key, value)
- this.map.set(key, value); → 키-값을 저장.
- 만약 동일한 키가 있으면 덮어쓰기됨.
- get(key)
- this.map.get(key); → 해당 키가 존재하면 값을 반환하고, 없으면 undefined 반환.
- delete(key)
- this.map.delete(key); → 해당 키가 있으면 삭제.
- print()
- console.log(this.map); → 현재 저장된 데이터 전체를 출력.
실행 결과
사과
Map(2) { 'apple' => '사과', 'grape' => '포도' }
- "banana"는 삭제되었기 때문에 "apple"과 "grape"만 남음.
왜 Map을 쓰는가?
여기서 Map을 쓴 이유는 일반 객체(Object)보다 해시 테이블 구조에 최적화되어 있기 때문이다.
특징 Object Map
| 키 타입 | 문자열만 가능 | 모든 타입 가능 (숫자, 객체 등) |
| 반복 | 키 순서를 보장하지 않음 | 입력 순서 보장 |
| 성능 | 키 개수가 많아지면 성능 저하 | 빠른 키 조회, 추가, 삭제 가능 |
결론
- insert() → 키-값 저장
- get() → 키로 값 찾기
- delete() → 특정 키 삭제
Set vs Map 차이점
print() → 전체 데이터 출력특징 Set Map
| 키 | 없음 (값만 저장) | 있음 (키-값 저장) |
| 중복 허용 | ❌ (중복 불가) | ⭕ (키만 유일하면 값은 중복 가능) |
| 사용 예 | 유니크한 값 저장 (태그, 방문 기록 등) | 키-값 저장 (딕셔너리, 캐싱 등) |
'Study > 코딩테스트(JS)' 카테고리의 다른 글
| 07. 큐 (0) | 2025.02.25 |
|---|---|
| 06. 스택 (0) | 2025.02.25 |
| 05.배열 (0) | 2025.02.18 |
| 04.코딩테스트 필수 문법 (1) | 2025.02.11 |
| 03.알고리즘의 효율 분석(BigO,시간&공간 복잡도) (0) | 2025.01.21 |



